The world has been full of sound since the Earth first acquired an atmosphere at least 3.8 billion years ago. Sound is the principle means with which humans communicate with each other. Hearing is one of the five senses with which humans perceive and explore the world in which they live. Sound in the form of music is one of the oldest and most widespread art forms that humans have created. All of this being so, it might come as a surprise to realise that the science of sound, acoustics, only really developed in any real sense in the eighteenth and nineteenth centuries. Acoustic derives from the Greek akoutikos = pertaining to hearing, from akoustos = heard, audible. Acoustics as the science of sound first appeared in the 1680s and meaning the acoustic properties of a building in 1885. However, the first tentative steps towards the science of acoustics took place in the Renaissance. Before we begin to examine those steps, we first need to look at what took place in antiquity, as this is the basis on which the Renaissance scholars built their theories.
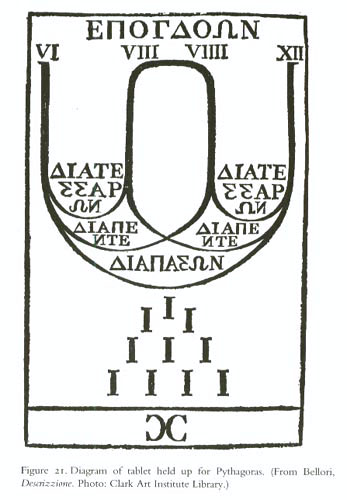
As usually this only refers to the developments within Europe, where there was historically no clear distinction between the terms we now use – sound, acoustics, music. Our first reference point in Pythagoras and his music theory. According to the well-known myth/legend/story, Pythagoras was walking past a smithy when he noticed the pitch of the sound made by the hammers varied with their weight and he decided to investigate the phenomenon. Pythagoras supposedly established that the weight of hammers or the length of strings on a monochord, a single stringed musical instrument, that produced a pleasing sound when sounded together, which we would now term harmonious, stood in whole number ratios to each other. So, a string twice as long as a given string will sound a note one octave lower than that of the given string:
In modern parlance, if a string sounds the note C when plucked, a string twice as long will sound a C an octave lower, so a ratio of 2:1. A perfect fourth has a ratio of 4:3 and a perfect fifth one of 3:2. The four numbers 1, 2, 3, 4 sum to ten making the Pythagorean tetractys.
The tetractys (Greek: τετρακτύς), is a triangular figure consisting of ten points arranged in four rows: one, two, three, and four points in each row, which is the geometrical representation of the fourth triangular number. As a mystical symbol, it was very important to the secret worship of Pythagoreanism. There were four seasons, and the number was also associated with planetary motions and music
Wikipedia

The Pythagoreans also propagated the theory of the harmony of the spheres, which claimed that the planets in their orbits created a harmonious musical scale, which depending on who’s telling the story is either inaudible to human ears or only audible to the enlightened sage.
As to be expected Aristotle had a theory on the nature of sound. He correctly attributes it to air pressure variations
Sound takes place when bodies strike the air, . . . by its being moved in a corresponding manner; the air being contracted and expanded and overtaken, and again struck by the impulses of the breath and the strings, for when air falls upon and strikes the air which is next to it, the air is carried forward with an impetus, and that which is contiguous to the first is carried onward; so that the same voice spreads every way as far as the motion of the air takes place.
—Aristotle (384–322 BCE), Treatise on Sound and Hearing[1]
In On Things Heard, attributed to Strato of Lampsacus (c. 335–c. 269 BCE), in the only extant version made up of long extracts included in the Commentary on Ptolemy’s Harmonics of Porphyry (c. 234–c. 305 CE) it is stated that the pitch is related to the frequency of vibrations of the air and to the speed of sound.

Ptolemaeus’ Harmonikon or Harmonics is not so well known as his astronomical or geographical works but did, as we will see, have an influence during the Renaissance and especially on Johannes Kepler. Like the Pythagoreans he argued for music intervals based on mathematical ratios. However, whereas the Pythagoreans saw the perfect fifth 3:2, as the basis of the musical scale, Ptolemaeus preferred perfect fourths 4:3 and octaves. His book closes with general thoughts on the relationships between harmony, the soul, and the planets (harmony of the spheres).
Turning from the philosophical and theoretical to the practical the De architectura of Vitruvius addresses the subject of acoustics in theatres. In Book V of his masterwork, Chapter 4 is titled Harmonic Principles. He apologises for using many Greek terms, explaining that there are not any Latin terms. There follows a lengthy discussion on the tones produced by the human voice and the intervals in singing. Chapter 5 is titled The Echea, Sounding Vessels in Theatres and discusses the production of bronze vessels designed to produce harmonics and their placement within the theatre to improve the acoustics.

Moving on to the education system, because of the Pythagorean association of music with arithmetic, it became part of the quadrivium the mathematical part of the seven liberal arts–arithmetic, geometry, music, astronomy–whereby music was regarded as arithmetic in motion and astronomy was geometry in motion.
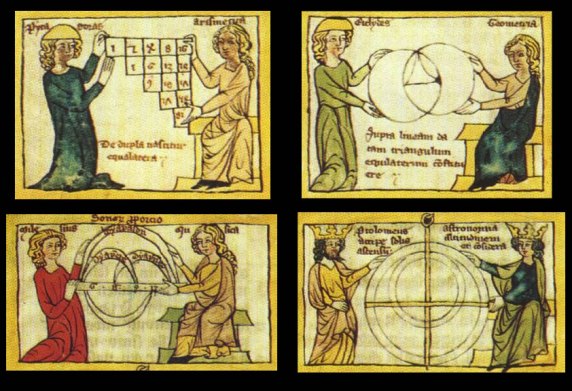
The standard text for teaching music as a part of the quadrivium at the medieval university was the De institutione musica by Boethius (c. 480–524 CE), one of the four texts that he wrote on the quadrivium subjects.

In “De Musica”, Boethius introduced the threefold classification of music:
- Musica mundana – music of the spheres/world; this “music” was not actually audible and was to be understood rather than heard
- Musica humana – harmony of human body and spiritual harmony
- Musica instrumentalis – instrumental music

Boethius’ Musica, Arithmetica, and Geometria were all printed for the first time in 1492 making the Pythagorean arithmetical theory of music widely available in the Renaissance.
As I explained in the episode of this series dealing with Vitruvius and De archtectura, it was also printed and published towards the end of the fifteenth century, not only in Latin but also fairly quickly in various vernacular languages. However, as I also pointed De archtectura was well-known in the Middle Ages but had little impact on medieval architecture. Having said that medieval churches often had acoustic jars, thought to have been inspired by Vitruvius’ enchae, inserted in strategic positions in the walls and flours to improve the acoustics. Unlike Vitruvius’ enchae, which were of bronze, the medieval acoustic jars were made of pottery.

We know from illustrations of instruments, people playing, singing, or dancing that there was a wide variety of music in the Middle Ages, and this is confirmed from written sources. However, the only form of medieval music from before eight-hundred CE, which we know in detail as music, is plain song or Gregorian chant. After eight hundred there are successive developments within a limited musical framework dominated by so-called modal music. There is a difference between modes and scales, which I’m not going to go into now. There was a definite development in the style of musical composition starting around the beginning of the fifteenth century and is regarded as the musical element of the Renaissance. To look more closely at this would however take us of course.
For our purposes the important development was initiated by Gioseffo Zarlino (1517–1590) a composer and musical theorist.

He was the first to prioritise the primacy of triad (a three note sequence) over the interval (two notes) that predominated in Pythagorean theory as central to Boethius. He also argued for various technical changes in intonation against the tradition Pythagorean system. Zarlino’s system as presented in his Istitutioni hamoniche (1558) was basically equivalent to that of Ptolemaeus in his Harmonikon.

Amongst his pupils was the lutenist, composer, and music theorist Vincenzo Galilei (1520–1591). Galilei disagreed with his teacher on many issues preferring the Pythagorean system, which he presented in his Dialogo della musica antica et della moderna (1581).

In defence of his system, he turned from pure theory to practical experiments with vibrating strings making him a pioneer in the systematic study of acoustic. He was assisted in his experiments by his, later more famous, son Galileo, and it is generally argued that Galileo acquired his interest in experimental physics working with his father in his youth.
The Galileis, father and son produced experimental proof that the ratio of an interval is proportional to string length, varies with the square root of the tension applied. Galileo extended his father’s experimental investigations of vibrating strings, looking at the effect of area of the cross-section, and the density of the material used. He almost certainly did this whilst he was still young, but the results of his father’s and his research were first published in his Discorsi e dimostrazioni matematiche intorno a due nuove scienze (Discourses and Mathematical Demonstrations Relating to Two New Sciences) in 1638.

At the end of the First Day in the Discorsi, Galileo begins a discussion on vibrations (pages 127 to 150 in the original). He starts by discussing his pendulum experiments including his slightly incorrect version of the law of the pendulum, Galileo’s observation of isochronism was accurate only for small swings. On page 138 he moves onto the whole theory of vibrating strings, pitch, consonance, and dissonance. He explains consonance as occurring when the pulses of the two notes frequently coincide on the tympanum of the ear. He also explains that one can demonstrate this visually by setting a set of pendula with strings in the same ratio as vibrating strings, 3:2 for the perfect fifth for example. It is obvious that Galileo has given the subject a lot of thought and carried out lots of experiment. He also describes a way to demonstrate the wave nature of sound:
The same phenomenon is observed to better advantage by fixing the base of the goblet upon the bottom of a rather large vessel of water filled nearly to the edge of the goblet; for if, as before, we sound the glass by friction of the finger, we shall see ripples spreading with the utmost regularity and with high speed to large distances about the glass. I have often remarked, in thus sounding a rather large glass nearly full with water, that at first the waves are spaced with great uniformity, and when, as sometimes happens, the tone of the glass jumps an octave higher I have noticed that at this moment each of the aforementioned waves divides into two; a phenomenon that shows clearly that the ratio involved in the octave [forma dell’ ottava] is two.
(Discorsi pp. 142-143)[2]
The work of Vincenzo and Galileo Galilei on acoustics is a classic example of what defines Renaissance science. They proceed from artisan knowledge, that of a working musician, Galileo was like his father a lutenist, on stringing and tuning an instrument and through careful experimental investigation turn it into scientific knowledge.
Although, Galileo discusses the factors that affect the pitch of a vibrating string–length, tension, cross-section, density–he doesn’t actually give a formula that combines the various factors; this was left up to the French mathematical scholar, Marin Mersenne ((1588–1648). Mersenne, who I have dealt with more fully here, personally knew Galileo and was a big fan of the Tuscan scholar’s work. He invested much effort into trying to persuade others to read Galileo’s books, which rather contradicts the popular image that Galileo was widely read in the seventeenth century. As I stated in my earlier post on him, Mersenne’s biggest contribution to science was in the field of acoustics, and I’m just going to quote what I wrote there:
It was, however, in the field of music, as the title quoted above would suggest, which had been considered as a branch of mathematics in the quadrivium since antiquity, and acoustics that Mersenne made his biggest contribution. This has led to him being labelled the “father of acoustics”, a label that long term readers of this blog will know that I reject, but one that does to some extent encapsulate his foundational contributions to the discipline. He wrote and published five books on the subject over a period of twenty years–Traité de l’harmonie universelle (1627); Questions harmoniques (1634); Les preludes de l’harmonie universelle (1634); Harmonie universelle (1636); Harmonicorum libri XII (1648)–of which his monumental (800 page) Harmonie universelle was the most important and most influential.
In this work Mersenne covers the full spectrum including the nature of sounds, movements, consonance, dissonance, genres, modes of composition, voice, singing, and all kinds of harmonic instruments. Of note is the fact that he looks at the articulation of sound by the human voice and not just the tones produced by instruments. He also twice tried to determine the speed of sound. The first time directly by measuring the elapse of time between observing the muzzle flash of a cannon and hearing the sound of the shot being fired. The value he determined 448 m/s was higher than the actual value of 342 m/s. In the second attempt, recorded in the Harmonie universelle (1636), he measured the time for the sound to echo back off a wall at a predetermined distance and recorded the value of 316 m/s. So, despite the primitive form of his experiment his values were certainly in the right range.
Mersenne also determined the correct formular for determining the frequency of a vibrating string, something that Galileo’s father Vincenzo (1520–1591) had worked on. This is now known as Mersenne’s Law and states that the frequency is inversely proportional to the length of the string, proportional to the square root of the stretching force, and inversely proportional to the square root of the mass per unit length.
The formula for the lowest frequency is
where f is the frequency [Hz], L is the length [m], F is the force [N] and μ is the mass per unit length [kg/m]. Source: Wikipedia
We now need to go back a little and look at the harmony of the spheres as propagated by both the Pythagoreans and Ptolemaeus, as this too experienced a new lease of life in the Renaissance. Tycho Brahe designed and built his research centre Uraniborg on the Island of Hven in the second half of the 1570s. All the dimensions of the plan and façade of the building as well as the layout of the gardens surrounding it were in the Pythagorean harmonic ratios, as befits a temple to celestial research.

The man who took the whole concept of the harmony of the spheres furthest was Johannes Kepler in his monumental Harmonices mundi libri V (1619). As the scholar, who contributed the most to the foundations of modern heliocentric astronomy, much more than Tycho Brahe or Copernicus, on whose work he built, Kepler is usually regarded as one of the early modern scientists, but he was in fact a quintessential Renaissance figure. Blending practical knowledge, mathematics, mysticism, and rock-solid empirical science he constructed a wonderfully bizarre and totally unique synthesis. Ninety nine percent of his work usually simply gets ignored and he gets presented as the man, who discovered the three laws of planetary motion, as if he simply pulled them out of his hat, but Harmonices mundi libri V is the wonderful Renaissance creation, 508 large format pages in the modern English translation, that delivered up the third of the laws Kepler’s Harmonic Law.
Kepler had already indicated in his Mysterium cosmographicum (1596) that he intended to fine tune his model of the cosmos, based on the five regular Platonic solids, with music or the harmony of the spheres.
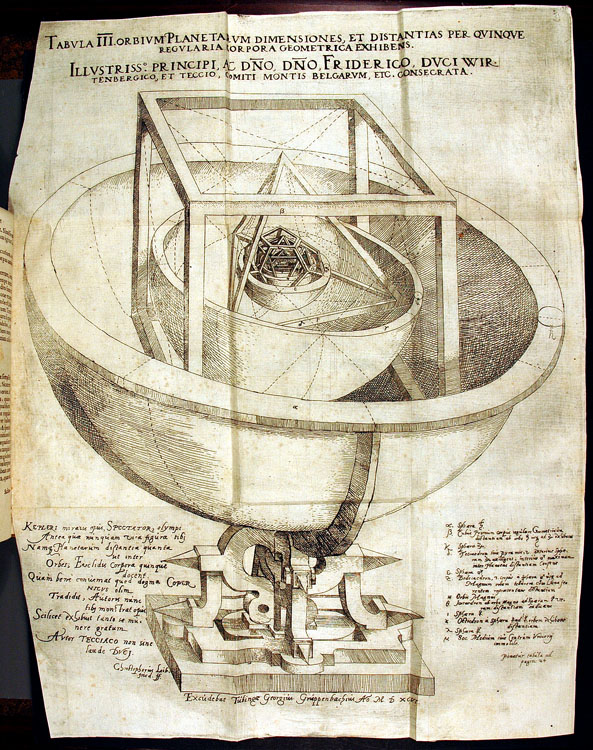
He began working on his theories already in the 1590s, expressing his interest in music theory in his correspondence with Michael Mästlin (1550–1631), Edmund Bruce (fl. 1597-1605) and Herwart von Hohenburg (1533–1622). He wrote to Bruce on 14th December 1599 of his intention to write a work with the title De harmonice mundi listing the contents, which are those that the book would eventually have, although it took him almost twenty years to write it. He saw his book as a direct competitor to or update of Ptolemaeus’ Harmonikon, even going so far as to borrow a Greek manuscript of Ptolemaeus’ book and translating parts of it himself. By following a basic Pythagorean line in his theories, Kepler was rejecting to more modern music theories that had come to dominate in the seventeenth century.
Books I & II Kepler deals with the construction of geometrical figures. In Book III he outlines Pythagorean music and number theory, as an introduction before presenting his own geometrical theory of consonance and dissonance based on numerical ratios of figures constructable with a straight edge and compass. In Book IV he applies his harmonic theories to his own more than somewhat deviant theories of astrology. It is in Book V that he now applies his theories to his model of the cosmos, beginning with the five Platonic solids then moving on to the motions of the planets, analysing all aspects of the planetary orbits for harmonious ratios.

All of this wonderfully bizarre theorising, in the end, delivered up Kepler’s third law of planetary motion his harmony law, perhaps the most important contribution to the mathematical theory of astronomy before Newton.
Newton, often regarded as the founder of much of modern science, was, himself, not immune to the allure of the Pythagorean theory of the harmony of the spheres, using it, as I outlined in an earlier post, to justify differentiating seven colours in the rainbow, seven colours, seven notes of the scale, a colour scheme that we still follow today.
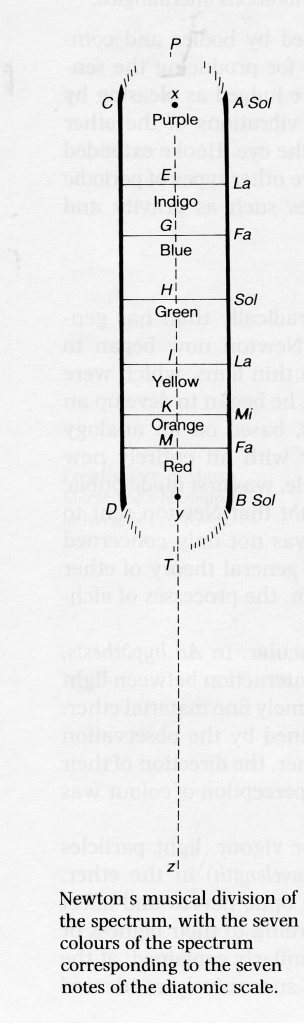
The Renaissance occupation with music theory yielded some strange fruit.
[1] “How Sound Propagates” (PDF). Princeton University Press.
[2] Dialogues Concerning Two New Sciences Galileo Galilei, translated by Henry Crew and Alfonso de Salvio, Dover, NY, 1954 p. 99
