This blog post is a modified version of two blog posts from my The emergence of modern astronomy–a complex mosaic series and yes it involves self plagiarism. I wrote it, rather than simply linking, because the content also belongs in this blog post series, which I wish to be complete and autonomous
Short popular presentations of the history of the origins of modern physics usually consist of three sections. In ancient Greece, Aristotle got almost everything wrong. In the Middle Ages, people clung religiously to Aristotle’s wrong theories. Then came Galileo and everything was light! A somewhat, sarcastic exaggeration but pretty close to the truth of what people like to believe and believe is the right verb because it bears little relation to what actually happened. You will note in my little parody that there is no mention of the Renaissance. This is because it just gets subsumed into the amorphous Middle Ages in this version of history. Galileo is always presented as a sort of messiah single handily casting a shining light into the dark reaches of medieval Aristotelianism and bringing forth, in a sort of virgin, birth modern physics.
In reality, whilst the considerations of what became modern physics are based on the concepts of Aristotle, there were major developments between the fourth century BCE and the early seventeenth century, especially during the Renaissance, changes of which Galileo was well aware and on which he built his, not always correct, contributions. In what follows I’m going to briefly outline the evolution of the theories of motion from Aristotle down to the seventeenth century; the theories of motion that then emerged being the bedrock on which Isaac Newton constructed his physics.
When talking of the history of physics it is important to note that what Aristotle meant with the term, one that he coined, is very different to the modern meaning, one that only began to emerge in the eighteenth century. For Aristotle his ta physika literally means “the natural things” and his physics means the study of all of nature, a study that is also non-mathematical. For Aristotle the objects of mathematics do not describe anything real, so mathematics can not be used to describe the real world. He does allow the use of mathematics in the so-called mixed sciences–astronomy, optics, harmonics (music or more accurately acoustics)–all of which we would include, at least in part, in a general definition of physics but for Aristotle were not part of his ta physika.
Central to Aristotle’s theory of nature was the establishment of the general principle of change that governs all natural bodies. For Aristotle motion is quite simply change of place. Aristotle complicates this simple picture in that he differentiates between celestial and terrestrial motion and between natural and violent or unnatural motion.
Simplest is his description of natural celestial motion, which is uniform circular motion, a concept that he inherited from Empedocles (c. 494 – c. 434 BCE, fl. 444–443 BCE) via his teacher Plato (c.425 BCE – 348/347 BCE). There is no violent or unnatural celestial motion. Aristotle’s theory of celestial motion is cosmology not astronomy and therefore not mathematical. The attempts to describe that motion mathematically are astronomical and thus not part of Aristotle’s physics.
Unlike celestial motion, both natural and violent terrestrial motion exist. For Aristotle, natural terrestrial motion is always perpendicular to the Earth’s surface and is the result of the four elements-earth, water, air, fire (another concept inherited from Empedocles)–striving to return to the natural places. So, the light elements–air and fire–travel upwards away from the Earth’s surface and the heavy elements–water and earth–fall downwards towards the Earth’s surface. In Latin this indication of heaviness is termed gravitas, object consisting principally of earth and/or water have gravitas and so they fall downwards.
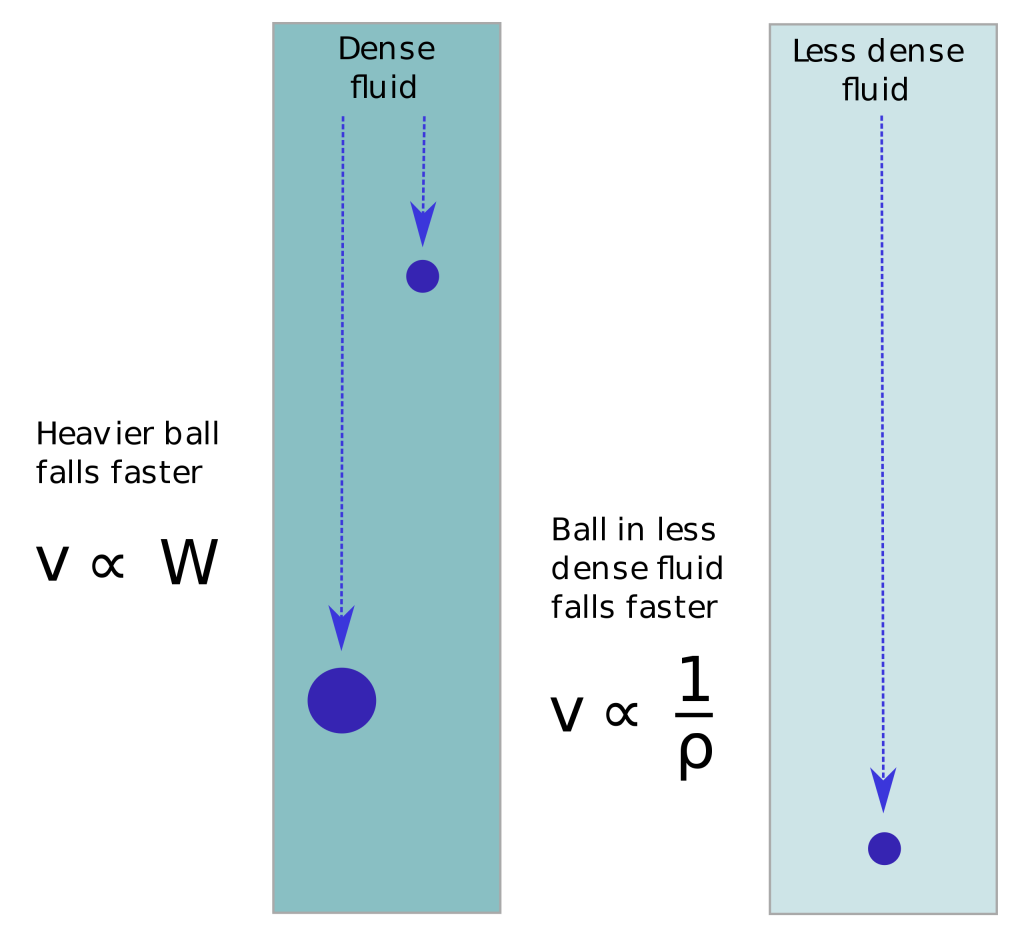
Violent terrestrial motion is any motion that is not natural motion and must be brought about by the application of force. Simplified for something to move, other than falling, it has to be pulled or pushed. For Aristotle, the only contactless motion is the fall of water and earth due to gravitas and the rise of air and fire to their natural place in the world, all other motion requires contact between the object being moved and whoever or whatever is doing the moving. As with much of Aristotle’s philosophy these concepts are based on empirical observation of the real world and are not so wrong, as they are often painted. Aristotle does not have a quantitative law of fall, but he asserts that objects fall at speed proportion to their weight and inversely proportional to the density of the fluid they are falling through. This is often contrasted with Galileo’s “correct” law of fall that all objects fall at the same speed, but Galileo’s law is only valid for a vacuum.
Aristotle has major problems with projectile motion. If you throw a ball or shoot and arrow, then according to Aristotle, as soon as the ball leaves your hand or the arrow the bowstring then it should immediately stop moving and fall to the ground, which it very obviously doesn’t. He got round the problem by claiming that the projectile parts the air as it flies, which then rushed round to the back of the object to prevent a vacuum forming and pushes the projectile forwards. An explanation that people found difficult to swallow and I suspect that even Aristotle found it less than satisfactory.
It is exactly here in his theory of projectile motion that Aristotle’s theories of terrestrial motion were first challenged and that already in the sixth century CE by the Alexandrian philosopher John Philoponus (c. 490–c. 570). Philoponus broke with the Aristotelian-Neoplatonic tradition of his own times and subjected Aristotle to severe criticism, writing commentaries on many of Aristotle’s major works and most importantly on Aristotle’s Physics. Whilst in general accepting Aristotle’s concept that for violent movement to take place a force must be applied but supplemented it by writing that in the case of projectiles, they acquired a motive power from the source providing the initial projection, which dissipated over time.
Philoponus didn’t restrict his concept to projectile motion, he also thought that the planets in their orbits had acquired the same motive when set in motion at the creation. Philoponus also rejects Aristotle’s theory of fall. It is obvious that one stone twice as heavy as another falls twice as fast. He apparently backed this up by doing empirical experiments. Showing that stones of differing weights fall at almost the same speed.
but this [view of Aristotle] is completely erroneous, and our view may be completely corroborated by actual observation more effectively than by any sort of verbal argument. For if you let fall from the same height two weights, one many times heavier than the other you will see that the ratio of the times required for the motion does not depend [solely] on the weights, but that the difference in time is very small. …
Because he fell into disgrace with the Church because of his religious writings, Philoponus’ Aristotle commentaries were little read in the West in the Early Middle Ages. However, they were read by Islamic scholars, such as Ibn Sina (c. 980–1037) (Avicenne), al-Baghdādī (c. 1080–1164), and al-Bitruji (died c. 1204), all adopted and modified Philoponus’ theory of projectile motion.

Whether directly from medieval manuscripts or through transmission by the translation movement, Philoponus’ work was known in Europe in the High Middle Ages. Amongst others, Thomas Aquinas (1225–1274) referenced but rejected it. It was the French scholastic philosopher, Jean Buridan (c. 1301–c. 1360), who adopted it and gave it both its final form and its name, impetus. Unlike Philoponus and his Islamic supporters, who thought that the implied motive force simply dissipated spontaneously over time, Buridan argued that the projectile was slowed and eventually brought to a halt by air resistance and gravity opposing its impetus. In Buridan’s more sophisticated version of Philoponus’ theory one can already see the seeds of the theory of inertia.

When a mover sets a body in motion he implants into it a certain impetus, that is, a certain force enabling a body to move in the direction in which the mover starts it, be it upwards, downwards, sidewards, or in a circle. The implanted impetus increases in the same ratio as the velocity. It is because of this impetus that a stone moves on after the thrower has ceased moving it. But because of the resistance of the air (and also because of the gravity of the stone) which strives to move it in the opposite direction to the motion caused by the impetus, the latter will weaken all the time. Therefore the motion of the stone will be gradually slower, and finally the impetus is so diminished or destroyed that the gravity of the stone prevails and moves the stone towards its natural place. In my opinion one can accept this explanation because the other explanations prove to be false whereas all phenomena agree with this one.
Buridan, like Philoponus and al-Bitruji, thought that impetus most the motive force of the planets, there being in the celestial sphere no air resistance of gravity to weaken it.
Impetus was established as the accepted theory of projectile motion at the beginning of the sixteenth century and it was the theory that Niccolò Fontana (c. 1500–1557), better known by his nickname, Tartaglia, used in his mathematical analysis of ballistics, his Nova scientia (1537), the first such book on the topic.

Here we have a classic example of Renaissance science, the application of the scientific approach to an artisanal practice, gunnery. Because he was using the theory of impetus and not the theory of inertia, Tartaglia’s theories of the flight path of cannon balls is wrong, but his book was widely read and highly influential, Galileo owned a heavily annotated copy.
Philoponus had also criticised Aristotle’s theory of fall and he was by no means the last medieval scholar to do so. The so-called Oxford Calculatores at Merton College, Thomas Bradwardine (c. 1300–1349), William of Heytesbury (c. 1313–c. 1372), Richard Swineshead (fl. c. 1340–1354) and John Dumbleton (c. 1310–c. 1349)–studied mechanics distinguishing between kinematics and dynamics, emphasising the former and investigating instantaneous velocity.

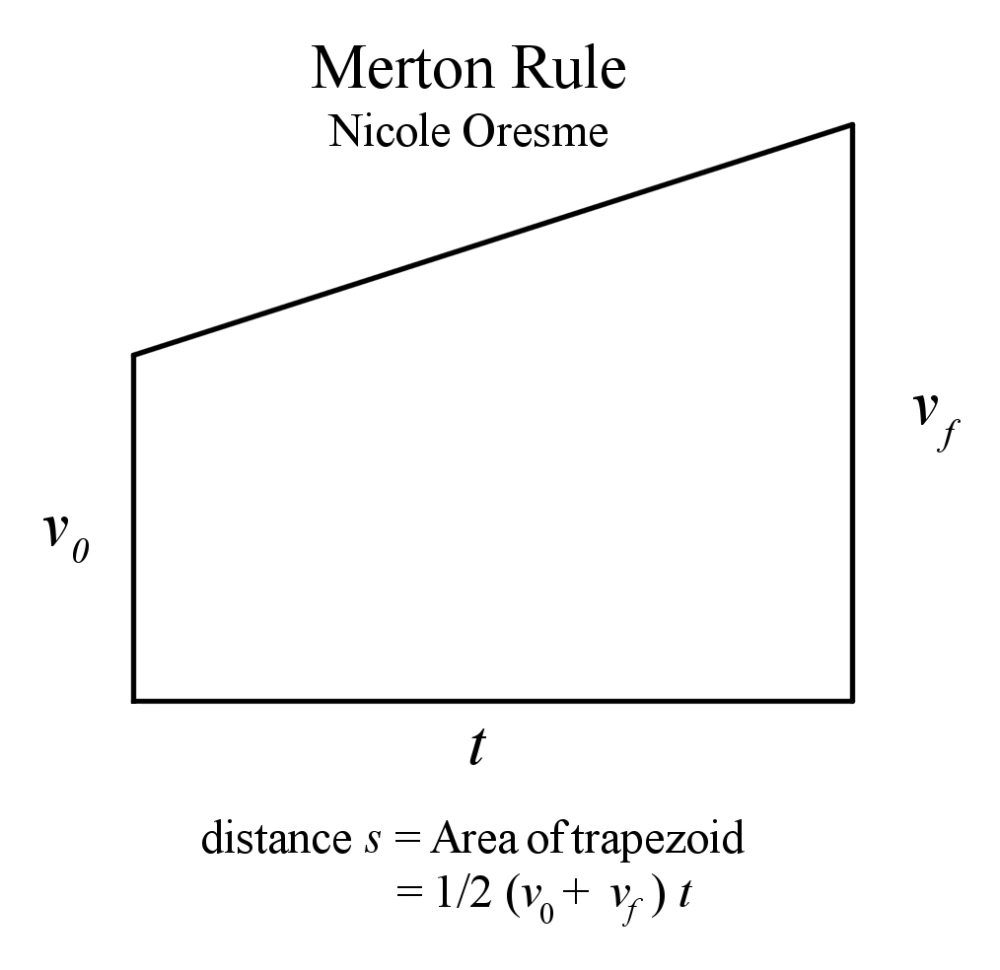
They were the first to formulate the mean speed theorem, an achievement usually accredited to Galileo. The mean speed theorem states that a uniformly accelerated body, starting from rest, travels the same distance as a body with uniform speed, whose speed in half the final velocity of the accelerated body. The theory lies at the heart of the laws of fall.
Nicole Oresme (c. 1320–1382), a Parisian colleague of Jean Buridan, in his own work on the concept of motion produced a graphical representation of the mean speed theorem,

as did Giovanni di Casali (c. 1320–after 1374), a Franciscan friar, who encountered the mathematical physics of the Oxford Calculatores, whilst working as a lecturer at Cambridge University around 1340. He wrote a treatise on his ideas on motion in 1346, which was published as De velocitate motus alterationis (On the Velocity of the Motion of Alteration) in Venice in 1351. His work on mathematical physics influenced scholars at the University of Padua and possibly later Galileo.
The most important work on the theories of motion by a Renaissance scholar is that of Giambattista Benedetti (1530–1590), a one-time pupil of Tartaglia. Addressing the law of fall, Benedetti in his Demonstratio proportionum motuum localium (1554) he argued that speed is dependent not on weight but specific gravity and that two objects of the same material, but different weights would fall at the same speed.

Benedetti brought an early version of the thought experiment, usually attributed to Galileo, of viewing two bodies falling separately or conjoined, in his case by a cord. Galileo considered a roof tile falling complete and then broken into two. Benedetti’s work was all done within the theory of impetus. Galileo’s first work on the topic, the unpublished De motu, written whilst he was still at the University of Pisa, also assumes the impetus theory and bears a strong resemblance to Benedetti’s work, which raises the question to what extent Galileo was acquainted with it. The opinions of the historians are divided on the topic.
Whereas Galileo almost certainly never threw balls off the Tower of Pisa, Simon Stevin (1548–1620), the mathematical engineer living and working in the newly established United Provinces, actually dropped lead balls of different weights from the thirty-foot-high church tower in Delft and determined empirically that they fell at the same speed, arriving at the ground at the same time. Stevin’s work was translated into both French and Latin and was widely read and highly influential in the France of Descartes, Mersenne, Gassendi et al.

There is a significant list of Renaissance scholars who reached and published the same conclusion, the Dominican priest Domingo de Soto (1494–1560) in Spain, Gerolamo Cardano (1501–1576), Benedetto Varchi (c. 1502–1565), Giuseppe Moletti (1531–1588) and Jacopo Mazzoni (1548–1598) in Italy. Girolamo Borro (1512–1592) one of Galileo’s teachers in Pisa, actually carried out empirical experiments to test Aristotle’s laws of fall, throwing objects of different material and the same weights out of a high window.
As can be seen from the above, when Galileo started working on the problems of motion towards the end of the sixteenth century, when he was still very much a Renaissance scientist, he was building on a strong tradition of criticisms and corrections to the Aristotelian theories stretching back to the early Middle Ages but also particularly vibrant in the sixteenth century. As already noted, Galileo earliest unpublished work, De Motu, was firmly entrenched in that tradition.
Of course, Galileo would go on to make significant advances in both projectile motion and the laws of fall but in the first he was definitely strongly influenced by another Renaissance mathematician, the Urbino aristocrat, Guidobaldo del Monte (1545–1607). Del Monte was one of the influential figures the young Galileo turned too for assistance at the beginning of his career. Impressed by the young Tuscan, Del Monte helped him to his appointment as professor for mathematics at the University of Pisa and again when he moved to the University of Padua.

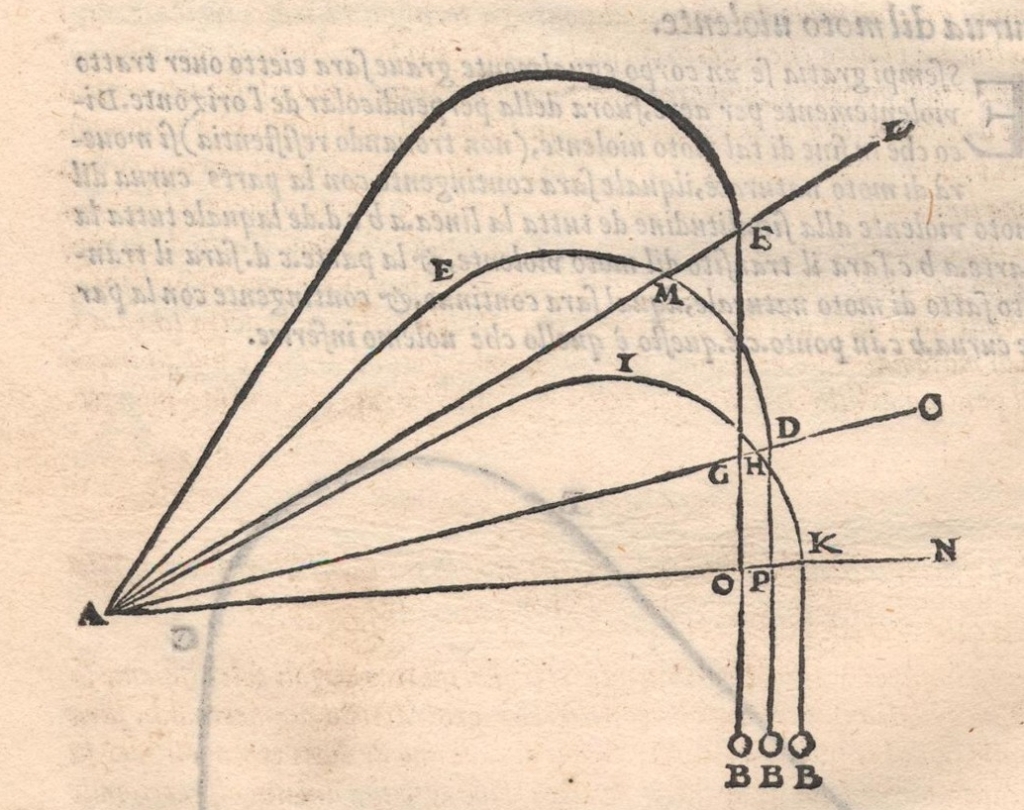
Galileo’s major contribution to the theory of projectile motion was the law of the parabola i.e., that the path of a projectile traces out a parabola. Galileo presents this in his Discorsi in 1638. However, it can be found in a notebook of del Monte’s from 1601, with a description of the proofs for this that are identical to those published by Galileo thirty-seven years later. The charitable explanation is that the two of them made this discovery together during one of Galileo’s visits to del Monte’s estate. The less charitable one is that Galileo borrowed del Monte’s results without acknowledgement, not the only time he would do such a thing.
The English polymath, Thomas Harriot (c.1560–1621) discovered the parabola law independently of del Monte/Galileo, but as with everything else didn’t publish his discovery. Bonaventura Cavalieri (1598–1647) did publish the parabola law, and in fact did so before Galileo, which brought an accusation of plagiarism from Galileo. Whether he borrowed the law from Galileo or discovered it independently is not known.

On the laws of fall, Galileo carried out his famous series of experiments using an inclined plane to verify what many others had confirmed during the preceding century. Here the problem is that his inclined plane would not give the level of accuracy of the results that he published. This led the historian of science and Galileo expert, Alexander Koryé (1892–1964), to hypothesise that the inclined plane was a purely hypothetical experiment that Galileo never actually carried out. The modern consensus is that Galileo did in fact carry out his experiments but massaged his results to make them fit the required theoretical values. As we have seen the mean speed theorem was already well established, as was the principle that objects of different weights fall at the same speed.
Galileo’s supposed other great contribution was the law of inertia. Moving from impetus to inertia was the major breakthrough in concepts of motion in the history of physics as it turns the whole problem on its head. Whereas Aristotle asked what moves things, the principle of inertia asks what stops them moving. Aristotle takes still stand as the natural state of objects that has to be changed, inertia takes motion of as the natural state of objects that has to be changed.
It is interesting to note that the supposedly modern scientist Galileo was in this concept trapped in the Greek paradigm of uniform circular motion being natural motion. Because of this, Galileo only defined inertia for circular motion:
“…all external impediments removed, a heavy body on a spherical surface concentric with the earth will maintain itself in that state in which it has been; if placed in a movement towards the west (for example), it will maintain itself in that movement.”[1]
Galileo’s addiction to the concept of uniform circular motion is also clear in his Dialogo, where he completely ignored Kepler’s laws of planetary motion, with their elliptical orbits maintaining the Copernican deferent-epicycle model
The Netherlander, Isaac Beeckman (1588–1637) had independently developed the concept of inertia already in 1614 and unlike Galileo he applied it to both circular and linear motion. Although, like Harriot, Beeckman never published, his work was well known to the physicist in Paris especially Descartes (1596–1650), Mersenne (1588–1648) and Gassendi (1592–1655). Newton (1642–1727) took the principle of inertia from Descarte, and not from Galileo as is often falsely claimed as his first law, and Descarte had it from Beeckman. Beeckman was an archetypal Renaissance scientist, an artisan who turned his attention to empirical experiments and science.
When one looks below the surface of the superficial accounts of the history of physics, it become clear the Renaissance scholar contributed substantially to the development of the theories of motion in the period leading up to the so-called scientific revolution.
[1] Stillman Drake, Discoveries and Opinions of Galileo, Doubleday, New York, 1957, p.113