### Thomas Digges (c. 1546–1595): England’s Premier Copernican and Visionary of the Boundless Universe
In the chronicles of Renaissance England’s emerging scientific landscape, one individual stands out: Thomas Digges. As the firstborn of Leonard Digges, a trailblazer in practical mathematics in England, Thomas was fated to carry on his father’s legacy. However, he not only perpetuated the mathematical pursuits inherited from his father but also broadened his scientific contributions into theoretical domains, positioning him as a crucial figure in Elizabethan mathematics and early astronomical thought. Like his father, who authored works for surveyors, craftsmen, and laborers, Thomas initially concentrated on practical applications before significantly pivoting toward theoretical inquiry, especially in relation to Copernican astronomy and the cosmos’s geometry.
#### **Formative Years and Education**
Thomas Digges’ formative years were riddled with obstacles that contributed to the resilience and inquisitiveness he later displayed in his academic endeavors. Born circa 1546, Thomas was the firstborn of Leonard Digges and Bridget Wilford. The political and financial difficulties faced by his father—arising from accusations of treason—significantly impacted the family. Although Leonard was ultimately pardoned, his properties and land were seized, leaving his sons without inheritance rights. It wasn’t until a parliamentary act in 1563 that Thomas and his younger brother, James, regained their legal standing.
Leonard’s passing before Thomas reached maturity meant that his education predominantly fell under the guidance of John Dee, England’s esteemed mathematician, astronomer, and counselor to Queen Elizabeth I. Dee, regarded as Thomas’ “second mathematical father,” had a profound impact on the young Digges. Their mutual respect is clearly illustrated in the works they produced following their joint observations of the 1572 supernova, a cosmic event that inspired contemporary astronomical pursuits. This intellectual collaboration defined Thomas’ path, leading him to a lifetime of pioneering contributions.
—
#### **Building on a Legacy: Digges and Mathematics**
Most of Thomas’ early published works served as expansions or reinterpretations of his father’s texts. One of the most notable collaborations between the two was *A Geometrical Practice Named Pantometria* (1571). Leonard’s portion stressed practical measurement techniques, providing guidelines for surveyors, builders, and artists. Conversely, Thomas presented advanced theoretical components, including his examination of the five Platonic solids and their geometric transformations into Archimedean solids. This *Mathematical Discourse* represented an early fusion of algebraic and geometric methods to investigate three-dimensional forms, showcasing both an expansive imagination and meticulous calculation.
Thomas transitioned from his father’s emphasis on practical trades to positioning mathematics as a universal and intellectual discipline. His *Mathematical Discourse* addressed sophisticated theorems on the properties of polyhedra, a topic aligning with broader Renaissance currents initiated by figures such as Piero della Francesca, Luca Pacioli, and Albrecht Dürer. What distinguished Digges, however, was his incorporation of algebra into geometric challenges, imparting a distinctly modern quality to his work for that era.
—
#### **The Road to Copernican Astronomy**
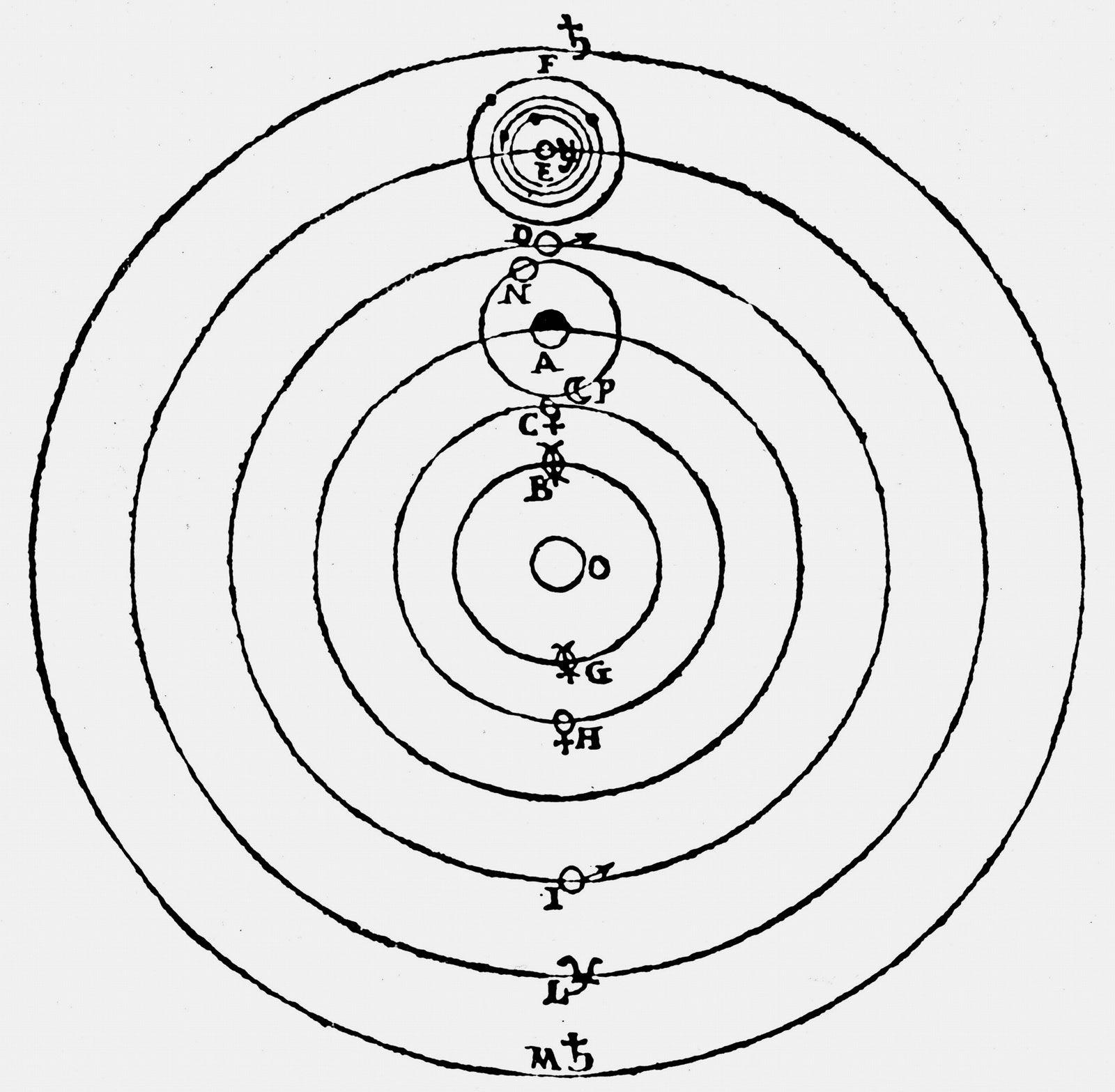
Thomas Digges is primarily remembered not solely for his mathematical prowess but as the first Englishman to express and champion a Copernican, heliocentric perspective. His interest in astronomy blossomed during his 1572 observations of the supernova in the constellation Cassiopeia. This celestial occurrence drove Digges to rethink the Ptolemaic geocentric model and engaged him in the Copernican debate prompted by the posthumous release of Nicolaus Copernicus’ *De revolutionibus orbium coelestium* in 1543.
In *Alae seu scalae mathematicae* (1573), Digges meticulously documented his observations of the supernova, employing advanced geometrical and trigonometric techniques to assert that it was a celestial entity beyond the Moon’s reach. This finding directly challenged the Aristotelian notion of the cosmos as permanent and unchanging, a widely held belief in his time. He also enhanced astronomical instruments, like the *radius astronomicus*, improving their accuracy for parallax measurements.
While his research on the supernova underscored his observational talent, Digges’ most groundbreaking insight lay in his overt endorsement of the Copernican model. In *A Perfit Description of the Caelestiall Orbes* (1576), an appendix to his father’s almanac, Thomas offered an annotated translation of the first book of Copernicus’ *De revolutionibus*. This publication represented the first comprehensive exposition of Copernican theory for an English readership. More provocatively, Digges diverged from Copernicus by positing the universe as infinite, with stars dispersed throughout an endless expanse rather than fixed within a crystalline sphere. His renowned depiction of this concept has