Today we celebrate the completion of the fourteenth journey around the Sun by the Renaissance Mathematicus. Yes folks, the Renaissance Mathematicus has now been dispensing history of science gems for fourteen long years. It seems that he’s here to stay, so what has he got to say for himself on this auspicious occasion?
Unlike thirteen, a year ago, or twelve, the year before, at first glance fourteen appears to be a rather boring number, not immediately suggesting a topic that we could spin out into today’s birthday blog post. However, appearances are deceptive. Fourteen delivers up a mathematical object that connects Archimedes, Luca Pacioli, Leonardo da Vinci, linear perspective, indirectly Paracelsus, Wenzel Jamnitzer, and Johannes Kepler all of them very much grist to the Renaissance Mathematicus mill. So, what is this wonderful mathematical object? It’s the truncated octahedron!
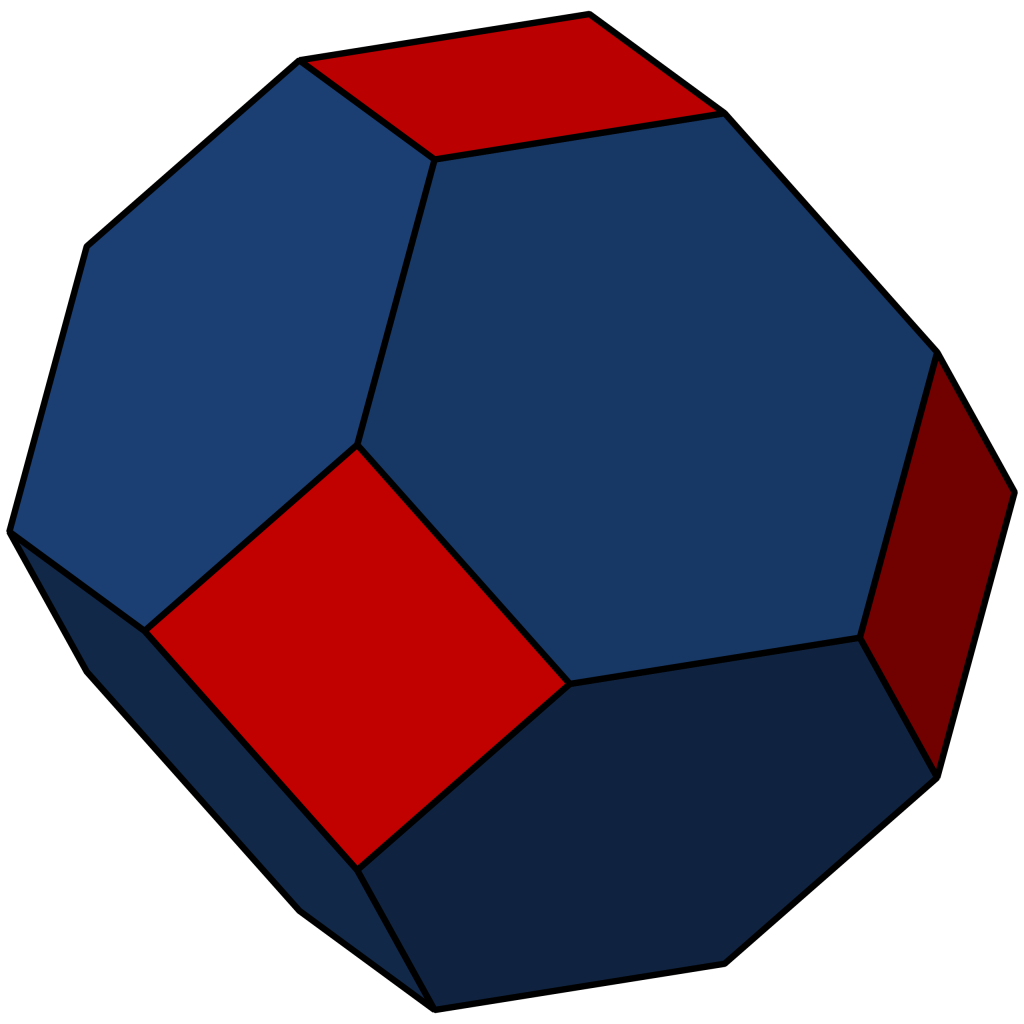
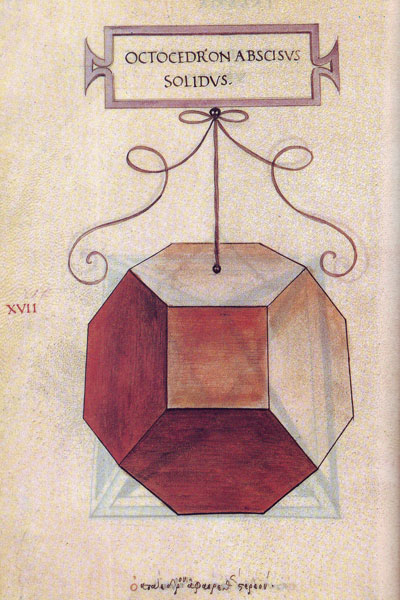
I can already hear a number of my readers muttering, what is a truncated octahedron when it’s at home? A truncated octahedron is a regular octahedron, which has six right square pyramids removed, one from each vertex. The resulting semi-regular solid has fourteen faces–eight hexagons and six squares.
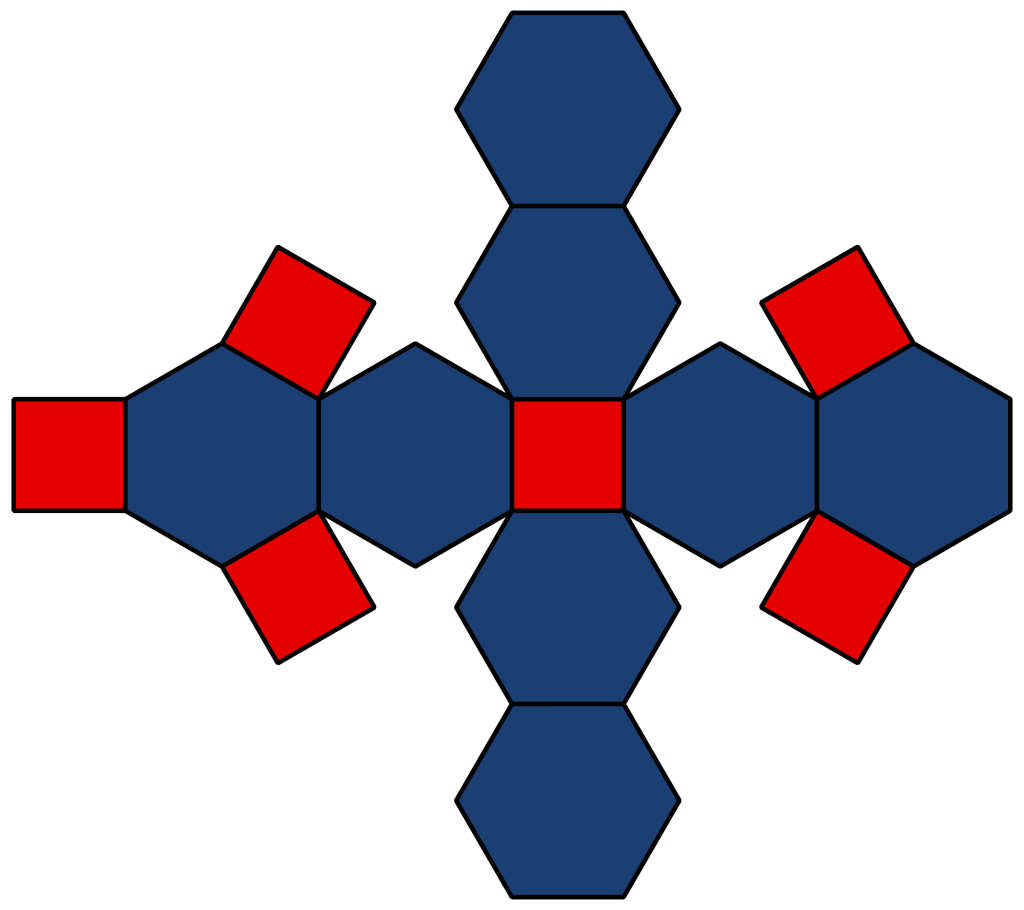
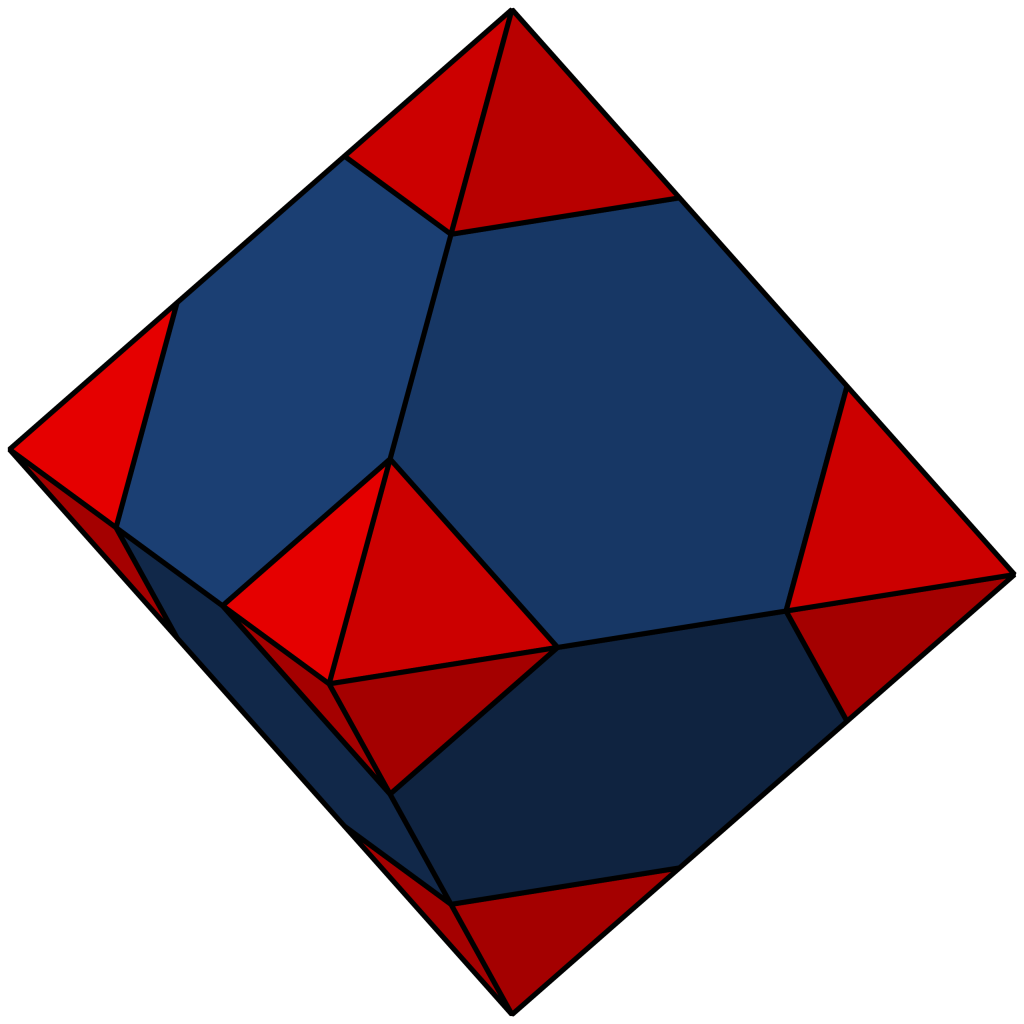
There are five regular geometrical solids, known as the Platonic solids–tetrahedron (4 faces), cube (6 faces), octahedron (8 faces), dodecahedron (12 faces), Icosahedron (20 faces).
In geometry a Platonic solid is a convex, regular polyhedron in three-dimensional Euclidian space. Being a regular polyhedron means that the faces are congruent (identical in shape and size) regular polygons (allangles congruent and all edges congruent), and the same number of faces meet at each vertex. There are only five such polyhedra. (Wikipedia)
Famously, in his Mysterium Cosmographicum, Kepler argued that there were and only could be six planets in his heliocentric system because there were separated by the five Platonic solid of which there could only be five.
The proof that there are only five Platonic solids is actually fairly easy, so I’ll leave it for my readers as an exercise.
They are known as the Platonic solids because, in his Timaeus, Plato hypothesized that the four classical elements were made of the first four–Earth/Cube, Water/Dodecahedron, Air/Octahedron, Fire/Tetrahedron. Much later the Icosahedron was attributed the Aristotle’s Aether.
There are thirteen semi-regular solids, known as the Archimedean solids. These are convex uniform polyhedra composed of regular polygons meeting in identical vertices, excluding the five Platonic solids. Like the truncated octahedron they are all basically modified forms of the Platonic solids. They are known as the Archimedean solids because Archimedes is said by Pappus to have discussed them in a now-lost work.
Following the discovery of linear perspective in the Renaissance it because a standard exercise for mathematici and artists to display their talent by producing three dimensional drawings of regular and semi-regular solids with the correct perspective.
Luca Pacioli (c.1447–1517) was one of the most important and influential Renaissance mathematici.
He wrote and published two major works, the first of which was his Summa de arithmetica, geometria, proportioni et proportionalita (Summary of arithmetic, geometry, proportions and proportionality) published in 1494.
Written in Italian it was the first printed book on algebra and included amongst other things an account of double entry bookkeeping. It also includes the erroneous claim that a general solution of the cubic equation was impossible. It is his second major work that concerns us here, it is his Divina proportione written in three parts between 1496 and 1498 but first published in 1509.
It is a book on mathematical proportions and their application to geometry, to linear perspective and to architecture. The third part of this book is a translation into Italian of Piero della Francesca’s Latin book De quinque corpibus regulaibus [On [the] Five Regular Solids], without acknowledgement.
There are two sections of illustration at the end of the book, the first section is letters of the alphabet drawn by Pacioli and the second section contains woodcuts, including the regular and semi-regular solids, drawn by Pacioli’s friend and mathematics student Leonardo da Vinci (1542–1519), which include both a solid and a skeletal drawing of our truncated octahedron.
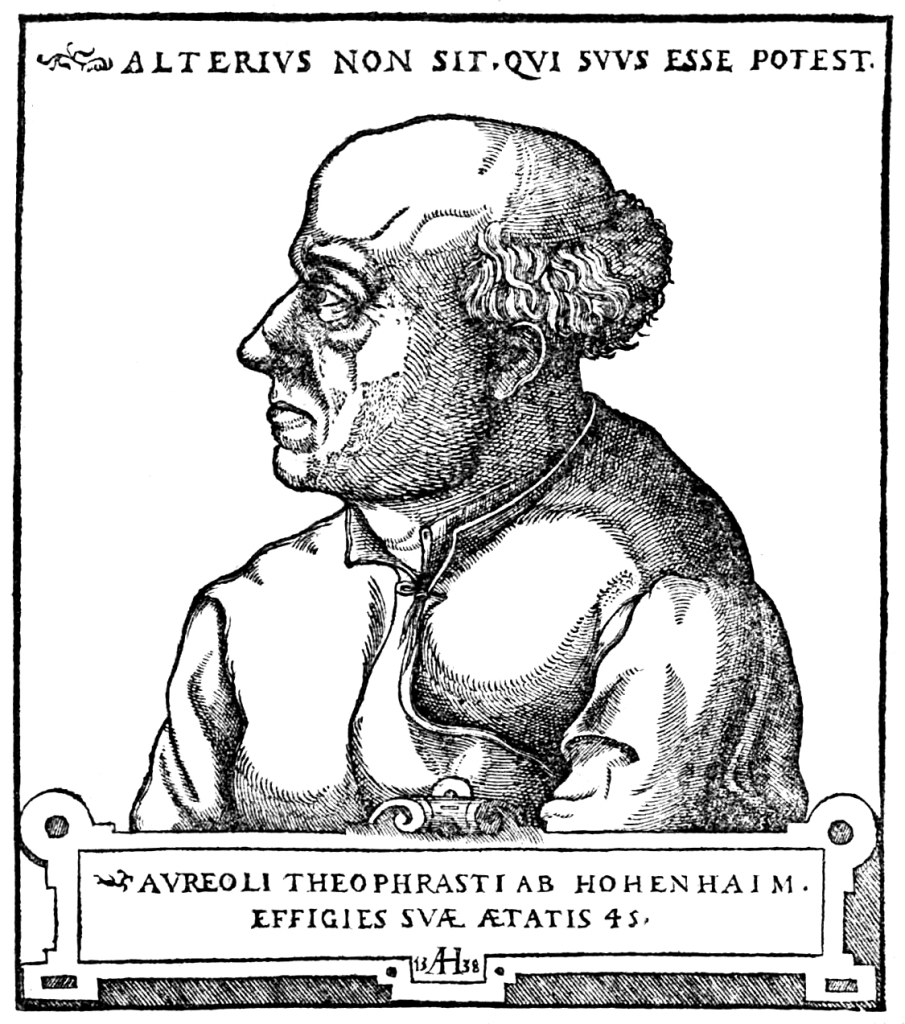
The only authenticated portrait of Paracelsus (c.1493–1541) was made by the Nürnberger engraver, mathematician, and cartographer Augustin Hirschvogel (1503–1553).
In 1543, Hirschvogel published a book on geometrical figures, his Geometria, which states on the title page:
DAS BVCH IST MEIN NAMEN
ALL FREYE KUNST AVS MIR ZUM ERSTEN KAMEN
ICH BRING ARCHITECTVRA VUD PERSPECTIVA ZUSAMEN
The Book is my name. All free art came first from me. I bring architecture and perspective together.
He includes a study of the truncated octahedron.
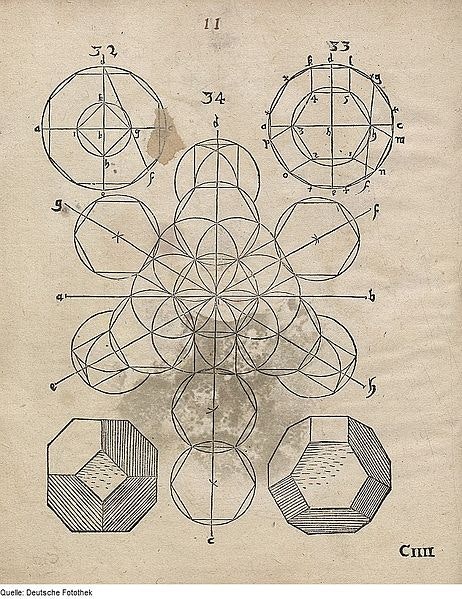
Another Nürnberger, who made an extensive study of the geometrical solids was goldsmith and engraver, Wenzel Jamnitzer (1597 or 1508–1585).
Wenzel Jamnitzer portrait by Nicolas Neufchatel Source: Wikimedia CommonsIn 1568 he published his extraordinary Perspectiva Corporum Regularium (The Regular Solids in Perspective), which has the subtitle:
Das ist Ein fleyssige Fürweysung, Wie die Fünff Regulirten Cörper, darvon Plato inn Timaeo, Unnd Euclides inn sein Elementis schreibt, etc. Durch einen sonderlichen, newen, behenden und gerechten weg, der vor nie im gebrauch ist gesehen worden, gar Künstlich inn die Perspectiva gebracht …
This is a studious demonstration, how the five regular solids, of which Plato in his Timaeus and Euclid in his Elements, wrote, etc. through a special, new, adroit, and correct way, that has never been seen in use before, brought artistically into perspective…
Jamnitzer, who covers far more than the five Platonic solids, presents each solid in its pure form and then develops it in numerous fascinating geometrical directions. Our truncated octahedron is one of the developments of the octahedron and is in turn geometrically developed.
Johannes Kepler (1571–1630) devoted the first two books of his Harmonices mundi libri V (The Harmony of the World in Five Books), published in 1619, to geometry.
The first book dealt with the construction of plane figures and contains, amongst many other things, his criticism that Dürer construction of a heptagon in his Underweysung der Messung mit dem Zirkel und Richtscheyt (Instruction in Measurement with Compass and Straightedge), published in 1525, is that it is at best a good approximation. The second book deals with the solids, including the Archimedean semi-regular solids, and contains the earliest known proof that there can only be thirteen of them. He also gave them the names that they still bear today. On the truncated octahedron he writes:
There are thirteen solid congruences which are perfect in an inferior degree. From these thirteen we obtain the Archimedean solids.[1]
[…]
Since the two kinds of plane figure will no longer include trigons the smallest figure involved will now be a tetragon. Three tetragon angles with one larger angle come to more than four right angles and by definition IX we know we cannot combine two tetragon angles with one larger angle, since only two of the larger figures will occur in the resultant solid. The case of one tetragon angle combined with two pentagon angles is rejected, by XXIII, but one tetragon angle will go with two hexagon angles, and six tetragons and eight hexagons will fit together to make a tessarkaedecahedron which I call a truncated octahedron (Octaëdron truncum). It is shown as number 5 in the diagram below.[2]
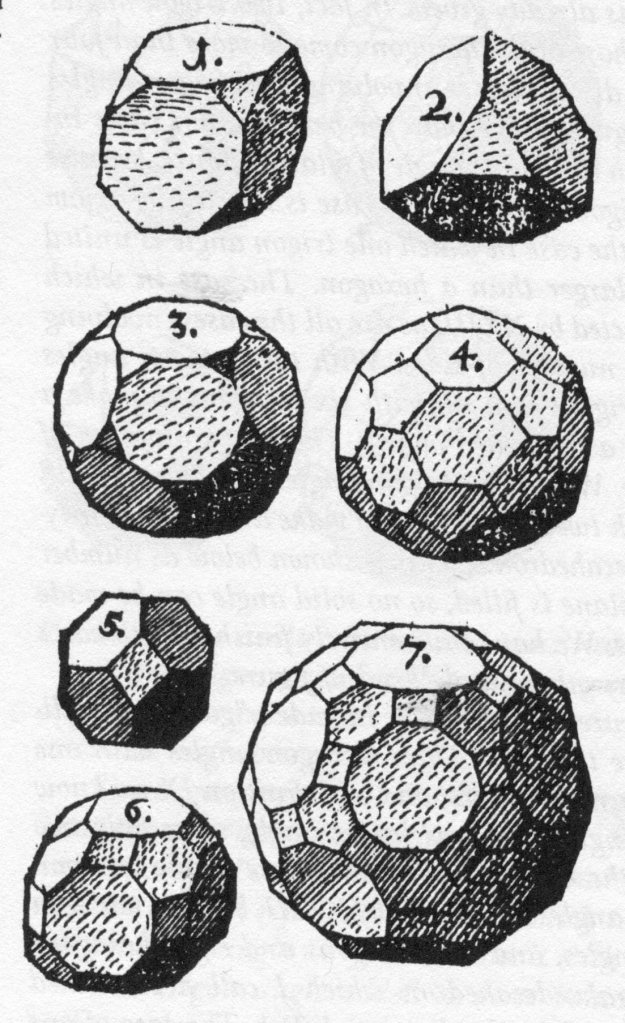
The tables and diagrams in The Harmony of the World were created by the young Wilhelm Schickard (1592–1635), whom Kepler had met in 1617 when he came to Württemburg to defend his mother against the charge of witchcraft. Schickard’s drawings cannot compete with those of Leonardo, Hirschvogel, and Jamnitzer.
The fourteen faces of the truncated octahedron stand here for fourteen years of this blog and maybe fourteen facets of the Renaissance mathematicus, who is definitely at best semi-regular.
[1] The Harmony of the World, p. 121
[2] The Harmony of the World, p. 121