No figure looms larger in the history of ancient mathematics than Archimedes, a name surrounded by a dense cloud of stories, myths, and legends. However, one should never lose sight of the fact that behind all the marvellous narratives about setting fire to enemy ships with burning mirrors and overturning others with giant levers, the real Archimedes was one of the greatest mathematicians who ever lived, and his work had a major impact on the newly emerging sciences in the sixteenth and seventeenth centuries.
Literally millions of words have been written over the centuries about Archimedes but if you ignore the posthumous hagiography, nearly all of which should be taken with a very large pinch of salt, then in realty we know almost nothing about the man. His supposed life dates c. 287–c. 212 BCE are based on something written by the Byzantine Greek historian, John Tzetzes (c.1110–1180 CE), so approximately fourteen hundred years after he lived. We do know that he was born in Syracuse on the island of Sicily, at the time a self-governing Greek city, and that he tells us in the Sand-Reckoner that his father was Phidias, an astronomer. Here, the reliable or solid facts end, the rest is just speculation. However, unlike Euclid nobody has ever doubted his existence.
Based on his surviving writings, Archimedes is credited with being a mathematician, engineer, astronomer, and inventor. He is usually referred to as a physicist, and although anachronistic, as I pointed out in the first episode of this series, the term in its modern usage was a nineteenth century minting by William Whewell, it is justified as several of his texts definitely fall withing the scope of modern physics, which played a significant role in his influence during the sixteenth and seventeenth centuries.
I shall ignore all of the war machines that Archimedes, the engineer, created for the defence of Syracuse, as described in the posthumous hagiographies, and concentrate instead on his know contributions to mathematics and science. Of course, the most popular presentation of Archimedes is the story of the crown, the bathtub, and running down the street shouting Eureka (Ancient Greek: εὕρηκα, Romanised: héurēka).
There is nothing remotely like this story in Archimedes own writings. It is also thought not to be real because the water displacement method of determining density that it supposedly led to, would be extremely difficult to realise due to the problems of accurately measuring the volume of water displaced. We will come to what he probably did later but first, feeling frivolous, I can’t resist repeating a terrible joke I first heard in my dim and distant youth:
Archimedes running down the street: Eureka! Eureka! …
Man, he passes: You dona smella too gooda youselfa!
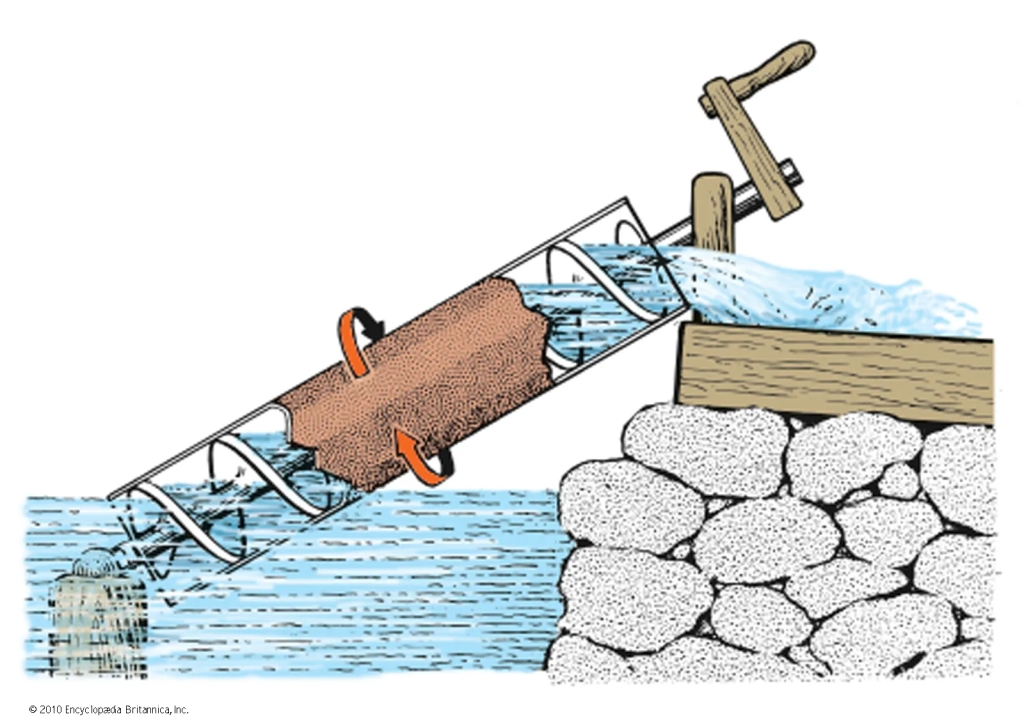
The so-called Archimedean Screw, which as the name suggests was named after him, a widespread method of raising water deserves at least a mention although there is no direct proof that he actually invented it.
As with other figures from antiquity there are works referenced by other writers that are no longer extant, in Archimedes’ case seven such works are recorded. The works that still exist, in the currently assumed order in which they were written, are Measurement of a Circle, The Sand Reckoner, On the Equilibrium of Planes, Quadrature of the Parabola, On the Sphere and Cylinder, On Spirals, On Conoids and Spheroids, On Floating Bodies, Ostomachion, The Cattle Problem, and The Method of Mechanical Theorems.
The Ostomachion is a geometrical puzzle similar to Tangram and The Cattle Problem is algebraic puzzle that requires the solution of a number of simultaneous Diophantine equations. The Cattle Problem was addressed to Eratosthenes and other Alexandrian mathematicians. The puzzles need not detain us here, but it is interesting to note that Archimedes had a playful side.
Measurement of a Circle is only a short fragment containing three propositions:
1) The area of any circle is equal to a right-angled triangle in which one of the sides about the right angle is equal to the radius, and the other to the circumference of the circle.
2) The area of a circle is to the square on its diameter as 11 to 14.
3) The ratio of the circumference of any circle to its diameter is greater than
.
Proposition three is his approximation of π and proposition two is actually derived from it, so the order can not be original. Both propositions one and three are examples of Archimedes using the method of exhaustion.
On the Equilibrium of Planes is in two books. Book one proves the law of the lever and contains propositions on the centre of gravity of the triangle and the trapezium. Book two has ten propositions on the centre of gravity of parabolic segments. This text would prove very important in the development of statics in the Early Modern Period.
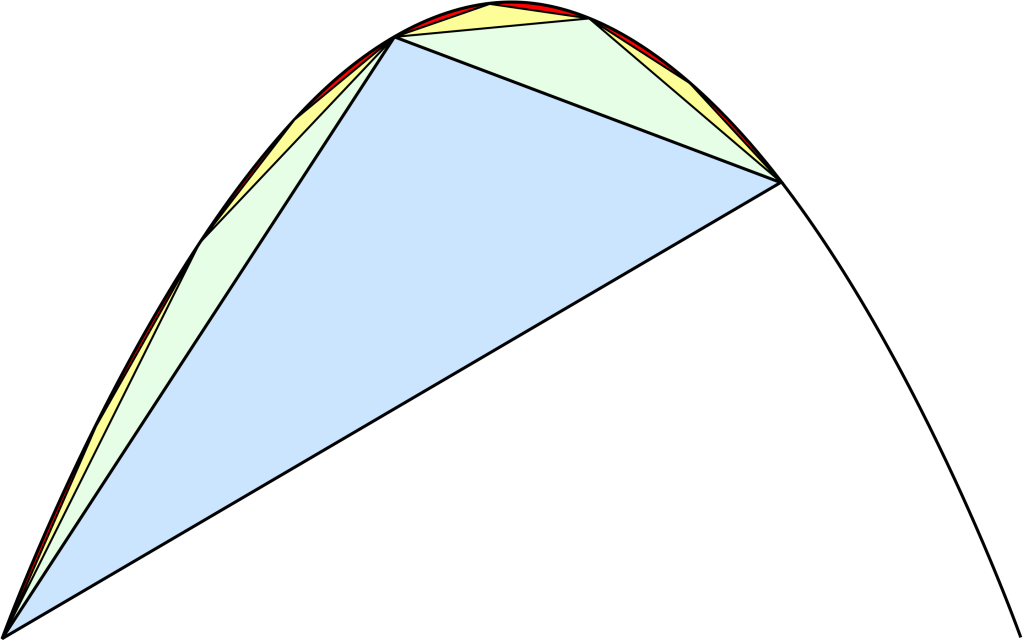
Quadrature of the Parabola has twenty-four propositions and culminates in the poof that the area enclosed by a parabola and a straight line is 4/3 the area of a triangle with equal base and height. He provides two proofs. The first proof is achieved by an application of the method of exhaustion The second s the dissection of the parabolic segment into infinitely many triangles, as shown in the figure below and then summing the infinite series. A very clear demonstration of Archimedes’ mathematical genius
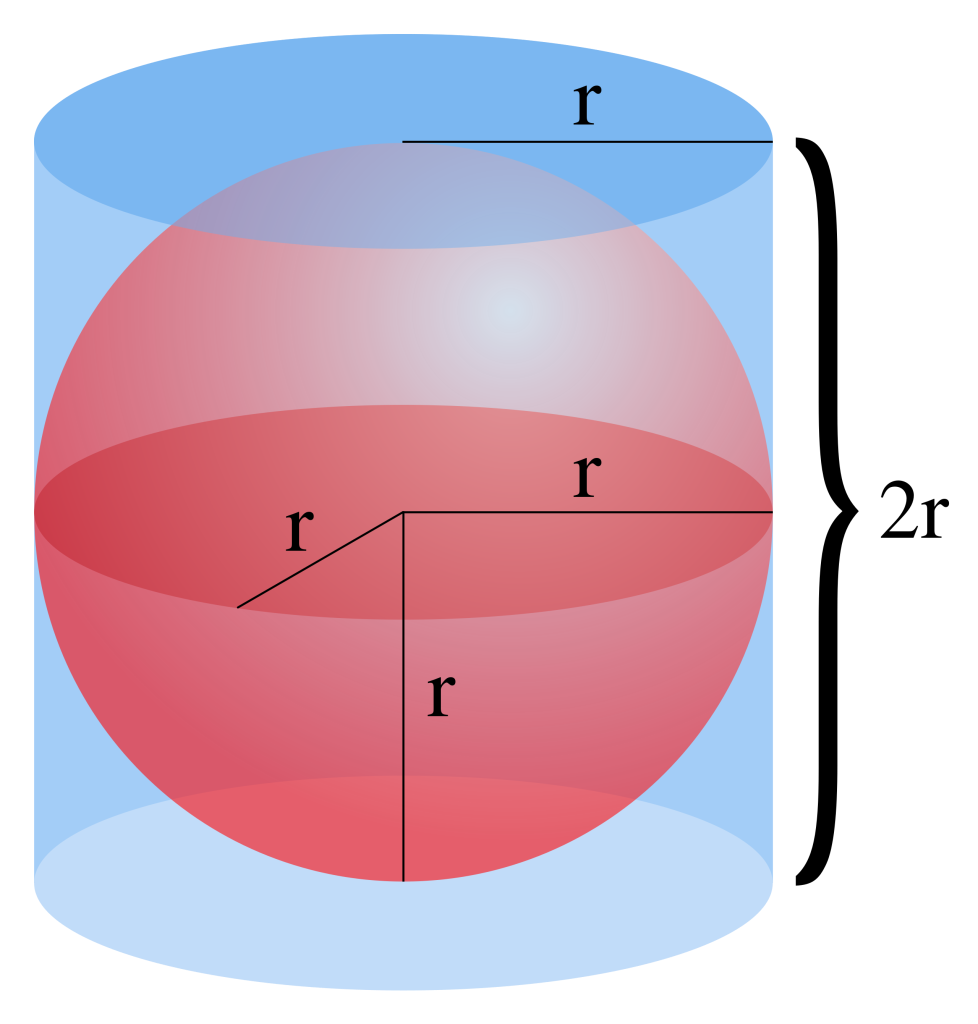
On the Sphere and Cylinder contains Archimedes’ famous proof that a sphere has 2/3 the volume and surface area of its circumscribing cylinder. It contains the earliest know explanation of how to find the volumes and surface areas of the two solids. Once again, he uses the method of exhaustion to achieve his results.
On Spirals defines what is now known as the Archimedean spiral, although it had been previously discussed by the astronomer and mathematician, Canon of Samos (c. 280–c. 220 BCE), as Archimedes acknowledges. He defines it thus:
If a straight line one extremity of which remains fixed is made to revolve at a uniform rate in a plane until it returns to the position from which it started, and if, at the same time as the straight line is revolving, a point moves at a uniform rate along the straight line, starting from the fixed extremity, the point will describe a spiral in the plane.
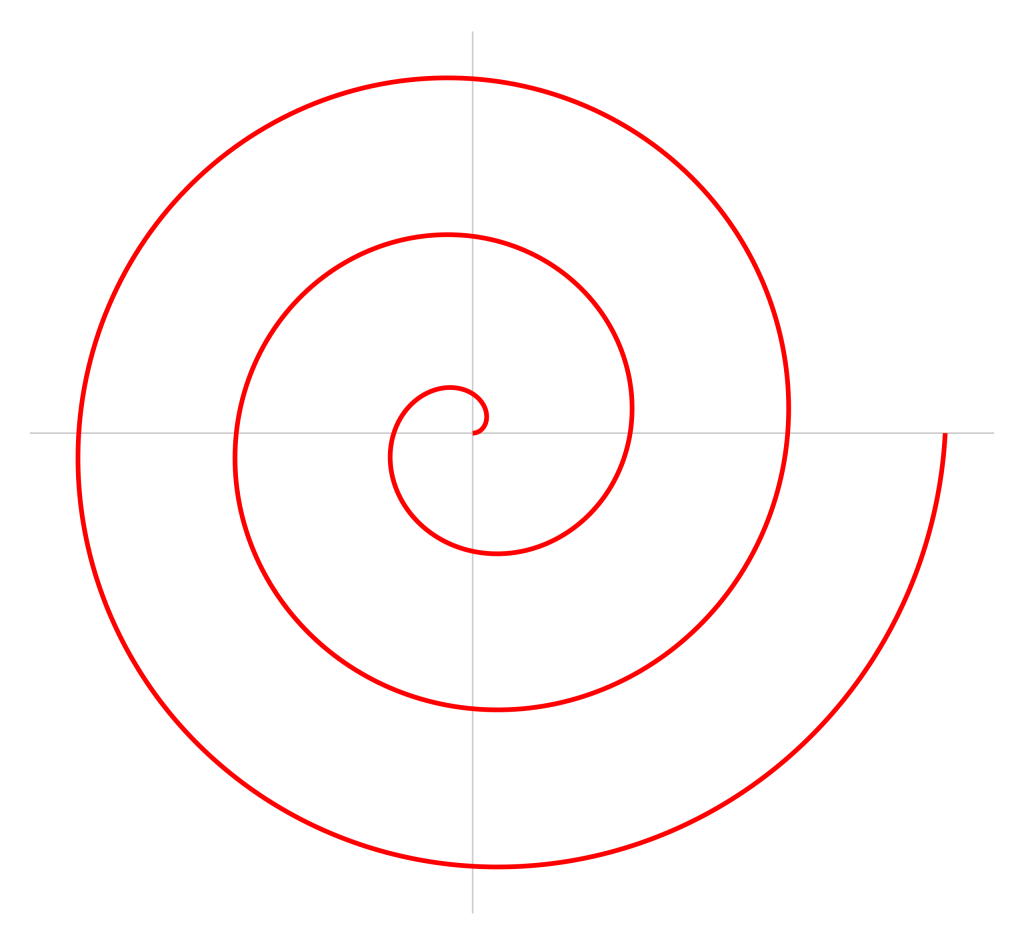
He uses the spiral to trisect and angle and also to square a circle. The Archimedean spiral is often confused in popular writing with the Golden spiral and the Fibonacci spiral.
In thirty-two propositions in On Conoids and Spheroids, Archimedes calculates the areas and volumes of sections of cones, spheres, and paraboloids. Once more making extensive use of the method of exhaustion.
On Floating Bodies could be said to be the most important of Archimedes’ surviving text, or at least the one with the most impact. It is the earliest known text on hydrostatics. Once again in two books, it investigates the position that various solids will assume went floating in a fluid, according to their form and the variations in their specific gravities. The second book is devoted to the floating properties of various paraboloids. The book contains the first statement of Archimedes’ Principle:
Any object, totally or partially immersed in a fluid or liquid, is buoyed up by a force equal to the weight of the fluid displaced by the object.
It is probably through the application of the principle utilising a hydrostatic balance, that is a balance with the pans resting in containers of fluid, that Archimedes actually solved the problem of whether the crown was pure gold or an alloy. This was the suggestion put followed by a young Galileo in his first ever original work, sent to Guidobaldo del Monte in 1586 in order to win his patronage.
As we will see later On Floating Bodies would go on to have a massive influence in the Early Modern period, when there was a major renaissance in interest in Archimedes’ work.
The brief sketches above demonstrate that Archimedes was a brilliant mathematician in what we would now term pure and applied mathematics or mathematical physics. There are two works that I haven’t dealt with yet, each of which is of a different nature to the works described above.
In The Sand Reckoner Archimedes develops a system for naming large numbers in order to determine the number of grains of sand needed to fill the cosmos. The normal Greek alpha-numerical number system being totally inadequate for the task. He proceeded by producing powers of the myriad (μυριάς — 10,000), nominally the largest number in the Greek counting system, so a myriad myriads (108) became the next step in his system followed by myriad-myriad myriad-myriads (1016). He then proceeded to potentiate (
You are now aware that the “universe” is the name given by most astronomers to the sphere the centre of which is the centre of the earth, while its radius is equal to the straight line between the centre of the sun and the centre of the earth. This is the common account (τὰ γραφόμενα) as you have heard from astronomers. But Aristarchus has brought out a book consisting of certain hypotheses, wherein it appears, as a consequence of the assumptions made, that the universe is many times greater than the “universe” just mentioned. His hypotheses are that the fixed stars and the sun remain unmoved, that the earth revolves about the sun on the circumference of a circle, the sun lying in the middle of the orbit, and that the sphere of the fixed stars, situated about the same centre as the sun, is so great that the circle in which he supposes the earth to revolve bears such a proportion to the distance of the fixed stars as the centre of the sphere bears to its surface.
The other text The Method of Mechanical Theorems, which was first discovered in 1906 on a palimpsest, a parchment scraped off and reused. The Method is a letter that he wrote to Eratosthenes in Alexandria. In this work Archimedes explains how to use indivisibles (geometrical equivalents of infinitesimals) to calculate areas and volumes. Archimedes did not consider that this method produced rigorous proofs, so having determined the solution using it he then redetermined using the method of exhaustion.
… certain things first became clear to me by a mechanical method, although they had to be proved by geometry afterwards because their investigation by the said method did not furnish an actual proof. But it is of course easier, when we have previously acquired, by the method, some knowledge of the questions, to supply the proof than it is to find it without any previous knowledge.
Although Archimedes was already a legend in antiquity because of his inventions his mathematical works received comparatively little attention. Isidore of Miletus (born c. 475 CE) produced the first comprehensive collation of them in Constantinople c. 530 CE. Also, in the sixth century, Eutocius of Ascalon (c. 480–c. 520) wrote commentaries on several of his mathematical works making them available to a wider readership.
Although his works were translated and known in the medieval period, it was first during the Renaissance that Archimedes’ mathematical works, in particular, On the Equilibrium of Planes and On Floating Bodies, began to have a major influence on the development of physics. Galileo was by no means the first or the only natural philosopher to consciously replace the qualitative physics of Aristotle with the mathematical physics of Archimedes setting in motion the mathematisation of science that is regarded as a key characteristic of the so-called scientific revolution.